Answer:
(a) The 90 percent confidence interval for the population mean yearly premium is ($10,974.53, $10983.47).
(b) The sample size required is 107.
Explanation:
(a)
The (1 - α)% confidence interval for population mean is:
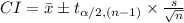
Given:
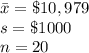
Compute the critical value of t for 90% confidence level as follows:
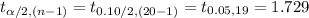
*Use a t-table.
Compute the 90% confidence interval for population mean as follows:
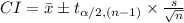
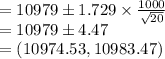
Thus, the 90 percent confidence interval for the population mean yearly premium is ($10,974.53, $10983.47).
(b)
The margin of error is provided as:
MOE = $250
The confidence level is, 99%.
The critical value of z for 99% confidence level is:
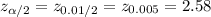
Compute the sample size as follows:
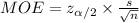
![n=[(z_(\alpha/2)* s)/(MOE) ]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/wecea0aqhytf2c960urj712bcf9n45y3fe.png)
![=[(2.58* 1000)/(250)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/zc4ku0ibaxbrq0u8vuswx19ck1zhcslwze.png)

Thus, the sample size required is 107.