Given:
Given that the irregular figure is broken into a triangle and a rectangle.
We need to determine the length b, the area of the triangle , the area of the rectangle and the area of the irregular figure.
Length of b:
The length of b , the base of the triangle is given by

Simplifying, we get;

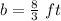
Thus, the length of the base of the triangle is

Area of the triangle:
The area of the triangle can be determined using the formula,
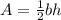
Substituting
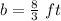 and
and
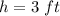 , we get;
, we get;
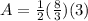
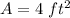
Thus, the area of the triangle is 4 square feet.
Area of the rectangle:
The area of the rectangle can be determined using the formula,

where l = 5 ft,
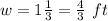 , we get;
, we get;
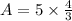
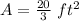
Thus, the area of the rectangle is
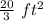
Area of the irregular figure:
The area of the irregular figure can be determined by adding the area of the triangle and the area of the rectangle.
Thus, we have;
Area = Area of the triangle + Area of the rectangle
Substituting the values, we have;
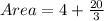
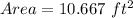
Thus, the area of the irregular figure is 10.667 square feet.