Question

A 7450 kg rocket blasts off vertically from the launch pad with a constant upward acceleration of 2.25 m/s2 and feels no appreciable air resistance. When it has reached a height of 500 m , its engines suddenly fail so that the only force acting on it is now gravity.a) What is the maximum height this rocket will reach above the launch pad?b) How much time after engine failure will elapse before the rocket comes crashing down to the launch pad?

Answer 1

Answer:

A) the maximum height this rocket will reach above the launch pad is 614.68 m

B) time elapsed after engine failure before the rocket comes crashing down to the launch pad is 16.025 sec.

Step-by-step explanation:

Detailed explanation and calculation is shown in the image below

Answer 2

a) 112.5 m

b) 15.81s

Step-by-step explanation:

a)We can use the following equation of motion to calculate the velocity v of the rocket at s = 500 m at a constant acceleration of a = 2.25 m/s2

`v^2 = 2as`

`v^2 = 2*2.25*500 = 2250`

`v = √(2250) = 47.4 m/s`

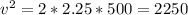
After the engine failure, the rocket is subjected to a constant deceleration of g = -10 m/s2 until it reaches its maximum height where speed is 0. Again if we use the same equation of motion we can calculate the vertical distance h traveled by the rocket after engine failure

`0^2 - v^2 = 2gh`

`-2250 = 2(-10)h`

`h = 2250/20 = 112.5 m`

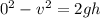
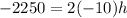
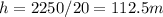
So the maximum height that the rocket could reach is 112.5 + 500 = 612.5 m

b) Using ground as base 0 reference, we have the following equation of motion in term of time when the rocket loses its engine:

`s + vt + gt^2/2 = 0`

`500 + 47.4t - 10t^2/2 = 0`

`5t^2 - 47.4t - 500 = 0`

`t= (-b \pm √(b^2 - 4ac))/(2a)`

`t= (47.4\pm √((-47.4)^2 - 4*(5)*(-500)))/(2*(5))`

`t= (47.4\pm110.67)/(10)`

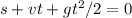
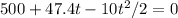
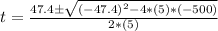
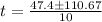
t = 15.81 or t = -6.33

Since t can only be positive we will pick t = 15.81s