Question

You want to rent an unfurnished one-bedroom apartment in Dallas next year. The mean monthly rent for a random sample of 14 apartments advertised in the local newspaper is $980. Assume the monthly rents in Dallas follow a Normal distribution with a standard deviation of $295. Find a 95% confidence interval for the mean monthly rent for unfurnished one-bedroom apartments available for rent in this community. (Round your answers to two decimal places.)

Answer 1

($825.47,$1134.53) is the required 95% confidence interval.

Explanation:

We are given the following in the question:

Sample mean,
`\bar{x}` = $980

Sample size, n = 14

Alpha, α = 0.05

Population standard deviation, σ = $295

95% Confidence interval:

`\bar{x} \pm z_(critical)(\sigma)/(√(n))`

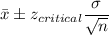
Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

`980 \pm 1.96((295)/(√(14)) ) \\\\= 980 \pm 154.53 \\\\= (825.47,1134.53)`

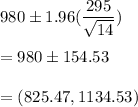
($825.47,$1134.53) is the 95% confidence interval for the mean monthly rent for unfurnished one-bedroom apartments.