Question

A bag contains 5 yellow blocks, 2 green blocks and 3 blue blocks. If you choose one block and then another block without putting the first one back in the bag, what is the probability that the first block will be green and the second will be yellow

Answer 1

The probability that the first block will be green and the second will be yellow is
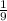`(1)/(9)` or 0.111.

Explanation:

We are given that a bag contains 5 yellow blocks, 2 green blocks and 3 blue blocks.

Also, we choose one block and then another block without putting the first one back in the bag.

Firstly, as we know that Probability of any event is given by ;

Probability of an event =
`\frac{\text{Favorable number of outcomes}}{\text{Total number of outcomes}}`

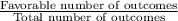
SO, Probability that the first block will be green =
`\frac{\text{Number of green blocks}}{\text{Total blocks in the bag}}`

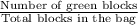
Here, Number of green blocks = 2

Total number of blocks in bag = 5 yellow + 2 green + 3 blue = 10 blocks

So, Probability that the first block will be green =
`(2)/(10)`

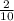
Similarly, Probability that the second block will be yellow =

`\frac{\text{Number of yellow blocks}}{\text{Total number of remaining blocks in the bag}}`

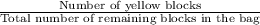
Here, Number of yellow blocks = 5

Total number of remaining blocks in bag = 10 - 1 = 9 blocks {because we haven't put the block back after choosing the first}

So, Probability that the second block will be yellow =
`(5)/(9)`

Now, Probability that the first block will be green and the second will be yellow =
`(2)/(10) * (5)/(9)`

=
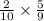
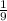`(1)/(9)` = 0.111

Hence, the required probability is 0.111.