Question

The fins are 90% efficient. Determine the minimum free-stream velocity the fan needs to supply to avoid overheating. Assume the flow is laminar over the entire finned surface of the transformer and check your assumption at the end. Assume the same convection heat transfer coefficient for the finned and unfinned area. Use 40 [C] for the film temperature.

Answer 1

The minimum required free stream velocity required to dissipate 12W via fins is V∞ = 0.0020378 m/s = 2.0378 mm/s.

Step-by-step explanation:

Given:-

- The dimension of transformer surface ( L , w , H ) = ( 10 cm long , 6.2 cm wide, 5 cm high )

- The dimensions of the fin : ( l , h , t ) = (10 cm long , 5 mm high, 2 mm thick )

- The total number of fins, n = 7

- The convection heat transfer coefficient of the finned and unfinned area = h.

- The efficiency of fins, ε = 0.9 ( 90% )

- The transformer fin base temperature, Tb = 60°C

- The free temperature of air, T∞ = 25°C

- The free stream velocity of air = U∞

Find:-

Determine the minimum free-stream velocity the fan needs to supply to avoid overheating. ( U∞ )

Solution:-

- Since the convection heat transfer coefficient of the finned and unfinned area i.e the fins and the transformer base are at the same temperature (Tb).

- The theoretical heat transfer ( Q_th ) rate from the fins can be calculated from the following convection cooling relation.

Q_th = h*As*[ Tb - T∞ ]

Where,

As : The total available surface area available for heat transfer.

• Surface area of the fins (As1)

As1 = n * { 2* [ ( l * h ) + ( t * h ) ] + ( l * t ) }

As1 = 7* { 2* [ ( 0.5 * 10 ) + ( 0.2 * 0.5 ) + ( 10 * 0.5 ) }

As1 = 106.4 cm^2 .... 0.01064 m^2

• Surface area of the unfinned part of base (As2)

As2 = Total base area - Finned top plane area

As2 = ( L * w ) - n* ( l * t ) = ( 10 * 6.2 ) - 7* ( 10 * 0.5 )

As2 = 27 cm^2 .... 0.0027 m^2

- Therefore, the total available surface area (As) is:

As = As1 + As2

As = 0.01064 + 0.0027

As = 0.01334 m^2

- The heat transfer coefficient (h) using convection heat transfer relation:

Q* ε = h*As*[ Tb - T∞ ]

h = Q* ε / [As*[ Tb - T∞ ] ]

h = (12*0.9) / [ 0.01334*( 60 - 25 ) ]

h = 23.13129 W/m^2K

- The air properties at film temperature:

T = 40 C

Viscosity ν = 1.6982 m^2 / s

Thermal conductivity, k = 0.027076 W/mK

Prandlt Number Pr = 0.71207

- The Nusselt number for the convection heat transfer for the transformer along the fins (Assumed flat plate):

Nu = h*L / k

Nu = 23.13129*0.1 / 0.027076

Nu = 85.43

- The correlation for Nusselt number between flow conditions and viscosity effects of the flow (Re & Pr) for a isothermal flat plate - Laminar Flow is given:

`Nu =  0.664*Re^(1)/(2) *Pr^(1)/(3) \\\\Re^(1)/(2) = (Nu)/(0.664*Pr^(1)/(3)) \\\\\\Re = \sqrt{(Nu)/(0.664*Pr^(1)/(3))} \\\\\\Re = \sqrt{(85.43063)/(0.664*0.71207^(1)/(3))}\\\\Re = 12.00`

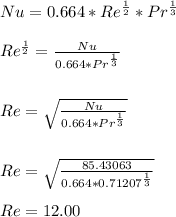
- The reynold number denotes the characteristic of the flow by the following relation:

Re = V∞*L / ν

V∞ = Re*ν / L

V∞ = 12*1.6982*10^-5 / 0.1

V∞ = 0.0020378 m/s .... = 2.0378 mm/s