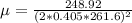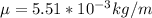Answer:
The linear mass density is of the string
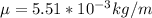
Step-by-step explanation:
From the question we are told that
The distance between wall and pulley is
The mass on the hook is
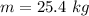
The frequency of oscillation is
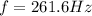
Generally, the frequency of oscillation is mathematically represented as
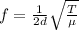
Where T is the tension mathematically represented as
T = mg
Substituting values
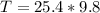
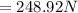
 is the mass linear density
is the mass linear density
Making
 the subject of the formula above
the subject of the formula above
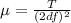
Substituting values