Question

Circle C has diameter AB. The coordinates of A are (5,1) and the coordinates of C are (6,10). Find the coordinates of B.

Answer 1

(7 , 19)

Explanation:

Centre is the midpoint of the diameter

C = Midpoint of AB

Let B: (x,y)

(6,10) = (x+5)/2, (y+1)/2

12 = x + 5

x = 7

20 = y + 1

y = 19

Answer 2

(7, 19)

Explanation:

We know that we are talking about circle C, which means that the center is point C. Since the diameter is AB, that means that AB goes through the center C and that center C is the midpoint of the segment AB.

Say the coordinates of B are (x, y). We can use the Midpoint Theorem to figure out B. The Midpoint Theorem states that for two points
`(x_1,y_1)` and
`(x_2,y_2)`, the coordinates of the midpoint are:
`((x_1+x_2)/(2) ,(y_1+y_2)/(2) )`.

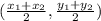Here, our two points are A(5, 1) and B(x, y). Then, the midpoint is:
`((5+x)/(2) ,(1+y)/(2) )`. We already know the midpoint is C(6, 10), so we can just set 6 equal to
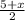`(5+x)/(2)` and set 10 equal to
`(1+y)/(2)`:

6 =
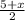`(5+x)/(2)` ⇒ 12 = 5 + x ⇒ x = 12 - 5 = 7

AND

10 =
`(1+y)/(2)` ⇒ 20 = 1 + y ⇒ y = 20 - 1 = 19

So, the coordinates of B is: (7, 19).

Hope this helps!