Question

) All human blood can be typed as one of O, A, B, or AB. The distribution of the type varies a bit with race. For African-Americans, here are the approximate probabilities that a person will have blood type O, A, B, or AB. In a group of 10 randomly chosen people, what is the probability that two or more of them have Type A blood? (Complement rule may be useful.)

Answer 1

The correct option is 1 - [(0.8)¹⁰+10*0.2*(0.8)⁹]= 0.6242

Explanation:

Hello!

Given the distribution of probabilities for blood types for African-Americans:

O: 0.4

A: 0.2

B: 0.32

AB: 0.08

A random sample of 10 African-American is chosen, what is the probability that 2 or more of them have Type A blood?

Let X represent "Number of African-Americans with Type A blood in a sample of 10.

Then you have two possible outcomes,

"Success" the person selected has Type A blood, with an associated probability p= 0.2

"Failure" the selected person doesn't have Type A blood, with an associated probability q= 0.8

(You can calculate it as "1-p" or adding all associated probabilities of the remaining blood types: 0.4+0.32+0.08)

Considering, that there is a fixed number of trials n=10, with only two possible outcomes: success and failure. Each experimental unit is independent of the rest and the probability of success remains constant p=0.2, you can say that this variable has a Binomial distribution:

X~Bi(n;p)

You can symbolize the asked probability as:

P(X≥2)

This expression includes the probabilities: X=2, X=3, X=4, X=5, X=6, X=7, X=8, X=9, X=10

And it's equal to

1 - P(X<2)

Where only the probabilities of X=0 and X=1 are included.

There are two ways of calculating this probability:

1) Using the formula:

`P(X)= (n!)/((n-X)!X!) *p^(x) * q^(n-x)`

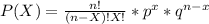
With this formula, you can calculate the point probability for each value of X=x₀ ∀ x₀=1, 2, 3, 4, 5, 6, 7, 8, 9, 10

So to reach the asked probability you can:

a) Calculate all probabilities included in the expression and add them:

P(X≥2)= P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) + P(X=8) + P(X=9) + X=10

b) Use the complement rule and calculate only two probabilities:

1 - P(X<2)= 1 - [P(X=0)+P(X=1)]

2) Using the tables of the binomial distribution.

These tables have the cumulative probabilities listed for n: P(X≤x₀)

Using the number of trials, the probability of success, and the expected value of X you can directly attain the corresponding cumulative probability without making any calculations.

>Since you are allowed to use the complement rule I'll show you how to calculate the probability using the formula:

P(X≥2) = 1 - P(X<2)= 1 - [P(X=0)+P(X=1)] ⇒

`P(X=0)= (10!)/((10-)0!0!) *0.2^(0) * 0.8^(10-0)= 0.1074`

`P(X=1)= (10!)/((10-1)!1!) *0.2^(1) * 0.8^(10-1)= 0.2684`

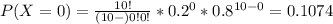
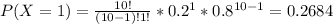
⇒ 1 - (0.1074+0.2684)= 0.6242

*-*

Using the table:

P(X≥2) = 1 - P(X<2)= 1 - P(X≤1)

You look in the corresponding table of n=10 p=0.2 for P(X≤1)= 0.3758

1 - P(X≤1)= 1 - 0.3758= 0.6242

*-*

Full text in attachment.

I hope it helps!