Answer:
The correct option is 1 - [(0.8)¹⁰+10*0.2*(0.8)⁹]= 0.6242
Explanation:
Hello!
Given the distribution of probabilities for blood types for African-Americans:
O: 0.4
A: 0.2
B: 0.32
AB: 0.08
A random sample of 10 African-American is chosen, what is the probability that 2 or more of them have Type A blood?
Let X represent "Number of African-Americans with Type A blood in a sample of 10.
Then you have two possible outcomes,
"Success" the person selected has Type A blood, with an associated probability p= 0.2
"Failure" the selected person doesn't have Type A blood, with an associated probability q= 0.8
(You can calculate it as "1-p" or adding all associated probabilities of the remaining blood types: 0.4+0.32+0.08)
Considering, that there is a fixed number of trials n=10, with only two possible outcomes: success and failure. Each experimental unit is independent of the rest and the probability of success remains constant p=0.2, you can say that this variable has a Binomial distribution:
X~Bi(n;p)
You can symbolize the asked probability as:
P(X≥2)
This expression includes the probabilities: X=2, X=3, X=4, X=5, X=6, X=7, X=8, X=9, X=10
And it's equal to
1 - P(X<2)
Where only the probabilities of X=0 and X=1 are included.
There are two ways of calculating this probability:
1) Using the formula:
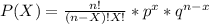
With this formula, you can calculate the point probability for each value of X=x₀ ∀ x₀=1, 2, 3, 4, 5, 6, 7, 8, 9, 10
So to reach the asked probability you can:
a) Calculate all probabilities included in the expression and add them:
P(X≥2)= P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X=7) + P(X=8) + P(X=9) + X=10
b) Use the complement rule and calculate only two probabilities:
1 - P(X<2)= 1 - [P(X=0)+P(X=1)]
2) Using the tables of the binomial distribution.
These tables have the cumulative probabilities listed for n: P(X≤x₀)
Using the number of trials, the probability of success, and the expected value of X you can directly attain the corresponding cumulative probability without making any calculations.
>Since you are allowed to use the complement rule I'll show you how to calculate the probability using the formula:
P(X≥2) = 1 - P(X<2)= 1 - [P(X=0)+P(X=1)] ⇒
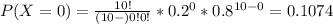
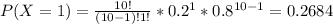
⇒ 1 - (0.1074+0.2684)= 0.6242
*-*
Using the table:
P(X≥2) = 1 - P(X<2)= 1 - P(X≤1)
You look in the corresponding table of n=10 p=0.2 for P(X≤1)= 0.3758
1 - P(X≤1)= 1 - 0.3758= 0.6242
*-*
Full text in attachment.
I hope it helps!