1 Answer

Greg Zimmers · Answer 1 · 2021-08-29T19:30:37+0000

Answer:

(C). (Probability of state A*Value in state A)+(Probability of state B*Value in state B)

Explanation:

The expected value of a probability distribution, E(X) is defined as:

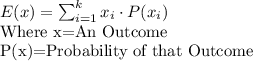
$E(x)=\sum_(i=1) ^(k) x_(i) \cdot P(x_(i))\\$Where x=An Outcome\\P(x)=Probability of that Outcome$

Given Outcome A and B, the Expected Value therefore is:

Expected Value = (Probability of state A*Value in state A)+(Probability of state B*Value in state B)

Please log in or register to add a comment.