Question

5.Richard Miyashiro purchased a condominium and obtained a 30-year loan of $196,000 at an annual interest rate of 8.20%. (Round your answers to the nearest cent.)

(a) What is the mortgage payment?
$

(b) What is the total of the payments over the life of the loan?
$

(c) Find the amount of interest paid on the mortgage loan over the 30 years.
$

6.
Marcel Thiessen purchased a home for $205,700 and obtained a 15-year, fixed-rate mortgage at 7% after paying a down payment of 10%. Of the first month's mortgage payment, how much is interest and how much is applied to the principal? (Round your answer to the nearest cent.)
interest $
applied to the principal $

Answer 1

5 a) PMT=$1,465.60

b) Total Payments=$527,616

c) Total Interest=$331,616

6a) Interest=$1,079.93

b) Principal=$584.07

Explanation:

a. Given the loan amount is $196,000, annual rate is 8.2% and the loan term is 30 years.

-The monthly mortgage payment can be calculated as follows:

`PMT=A(((r/n))/(1-(1+(r)/(n))^(-nt)))`

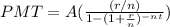
Where:

• PMT is the monthly mortgage payment
• r is the annual interest rate
• n,t is the number of annual payments and time in years respectively

-We substitute to solve for PMT:

`PMT=A(((r/n))/(1-(1+(r)/(n))^(-nt)))\\\\=196000[((0.082/12))/(1-(1+(0.082)/(12))^(-12*30))]\\\\=\$1,465.60`

Hence, the monthly mortgage payment is $1,465.60

b. The total number of payments is obtained by multiplying the total number of payments by the amount of each payment:

`\sum(payments)=PMT* nt\\\\=1465.60* 12* 30\\\\=\$527,616.00`

Hence, the total amount of payments is $527,616

c. The amount of interest paid over the loan's term is obtained by subtracting the principal loan amount from the total payments made:

`Interest=Payments-Principal\\\\=527,616.00-196,000.00\\\\=\$331,616`

Hence, an interest amount of $331,616 is paid over the loan's term.

6 a) We first obtain the effective loan amount by subtracting the down-payment:

`Loan \ Amount= Regular \ Price -Downpayment\\\\=205700-0.1(205700)\\\\=\$185,130`

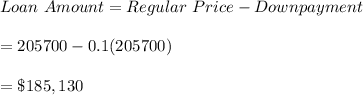
The interest paid on the first mortgage payment is calculated as below:

`I=(r)/(n)* P\\\\I=Interest\\r=interest \ rate\\n=Payments \ per \ year\\P=Outstanding \ loan \ balance\\\\\therefore I=(0.07)/(12)* 185130\\\\=\$1,079.93`

Hence, the amount of interest in the first payment is $1,079.93

b. The amount of principal repaid is obtained by subtracting the interest amount from the monthly mortgage payments;

`Principal \ Paid=PMT-Interest\\\\PMT=A[((r/n))/(1-(1+(r)/(n))^(-nt))]\\\\=185130[((0.07/12))/(1-(1+(0.07)/(12))^(-180))\\\\=1664.00\\\\\\Principal \ Paid=1664.00-1079.93\\\\=\$584.07`

Hence, the amount of principal applied is $584.07