Answer:
5 a) PMT=$1,465.60
b) Total Payments=$527,616
c) Total Interest=$331,616
6a) Interest=$1,079.93
b) Principal=$584.07
Explanation:
a. Given the loan amount is $196,000, annual rate is 8.2% and the loan term is 30 years.
-The monthly mortgage payment can be calculated as follows:
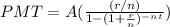
Where:
- PMT is the monthly mortgage payment
- r is the annual interest rate
- n,t is the number of annual payments and time in years respectively
-We substitute to solve for PMT:
![PMT=A(((r/n))/(1-(1+(r)/(n))^(-nt)))\\\\=196000[((0.082/12))/(1-(1+(0.082)/(12))^(-12*30))]\\\\=\$1,465.60](https://img.qammunity.org/2021/formulas/mathematics/college/hf48z2w4e599a6d62gtf4ig76u28mm6bht.png)
Hence, the monthly mortgage payment is $1,465.60
b. The total number of payments is obtained by multiplying the total number of payments by the amount of each payment:
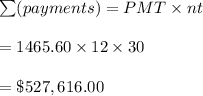
Hence, the total amount of payments is $527,616
c. The amount of interest paid over the loan's term is obtained by subtracting the principal loan amount from the total payments made:

Hence, an interest amount of $331,616 is paid over the loan's term.
6 a) We first obtain the effective loan amount by subtracting the down-payment:
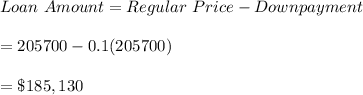
The interest paid on the first mortgage payment is calculated as below:

Hence, the amount of interest in the first payment is $1,079.93
b. The amount of principal repaid is obtained by subtracting the interest amount from the monthly mortgage payments;
![Principal \ Paid=PMT-Interest\\\\PMT=A[((r/n))/(1-(1+(r)/(n))^(-nt))]\\\\=185130[((0.07/12))/(1-(1+(0.07)/(12))^(-180))\\\\=1664.00\\\\\\Principal \ Paid=1664.00-1079.93\\\\=\$584.07](https://img.qammunity.org/2021/formulas/mathematics/college/w0abqaqf65ouc7yux8mnninrajbliyfedg.png)
Hence, the amount of principal applied is $584.07