Question

A double-concave (thickest at the edges, thinnest in the middle) thin lens is made of glass with an index of refraction of 1.6. The radius of curvature of the left and right faces of the lens are 65 cm and 75 cm, respectively. The object lies to the left of the lens. What is the focal length of the lens

Answer 1

- 58 cm

Step-by-step explanation:

refractive index, n = 1.6

radius of curvature of left face, R1 = - 65 cm

Radius of curvature of the right face, R2 = 75 cm

Use the lens maker's formula

`(1)/(f)=\left ( n-1 \right )* \left ( (1)/(R_(1))-(1)/(R_(2)) \right )`

`(1)/(f)=\left ( 1.6-1 \right )* \left ( -(1)/(65)-(1)/(75) \right )`

`(1)/(f)=\left ( 0.6 \right )* \left ( (-75-65)/(75* 65)\right )`

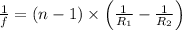
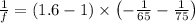
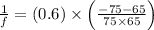
f = - 58 cm

Thus, the focal length of the lens is - 58 cm.