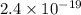Answer:
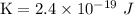
Step-by-step explanation:
The electric field inside a parallel plate capacitor is
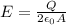
where A is the area of one of the plates, and Q is the charge on the capacitor.
The electric force on the electron is
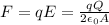
where q is the charge of the electron.
By definition the capacitance of the capacitor is given by
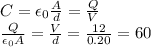
Plugging this identity into the force equation above gives
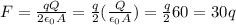
The work done by this force is equal to change in kinetic energy.
W = Fx = (30q)(0.05) = 1.5q = K
The charge of the electron is
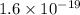
Therefore, the kinetic energy is