Question

In a mass spectrometer, a singly ionized 24Mg ion has a mass equal to 3.983 10-26 kg and is accelerated through a 3.00-kV potential difference. It then enters a region where it is deflected by a magnetic field of 526 G. Find the radius of curvature of the ion's orbit. Note: There are 10,000 G in 1 T and 1,000 V in 1 kV.

Answer 1

The radius of curvature of the ion's orbit is 0.59 meters

Step-by-step explanation:

Given that,

Mass of the 24 Mg ion,
`m=3.983* 10^(-26)\ kg`

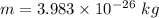
Potential difference, V = 3 kV

Magnetic field, B = 526 G

Charge on single ionized ion,
`q=1.6* 10^(-19)\ C`

The radius of the the path traveled by the charge is circular. Its radius is given by :

`r=(mv)/(Bq)`

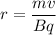
v is speed of particle.

v can be calculated using conservation of energy as :

`(1)/(2)mv^2=qV\\\\v=\sqrt{(2qV)/(m)} \\\\v=\sqrt{(2* 1.6* 10^(-19)* 2* 10^3)/(3.983 * 10^(-26))} \\\\v=1.26* 10^5\ m/s`

Radius,

`r=(3.983 * 10^(-26)* 1.26* 10^5)/(0.0526* 1.6* 10^(-19))\\\\r=0.59\ m`

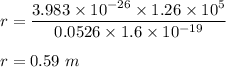
So, the radius of curvature of the ion's orbit is 0.59 meters.