Question

In a game of roulette, Jorge places 170 bets of each on the number 3. A win pays off with odds 35:1 and on any one spin there is a probability that 3 will be the winning number. Among the 170 bets, what is the minimum number of wins needed for Jorge to make a profit? Estimate the probability that Jorge will make a profit.

Answer 1

probability that Jorge makes a profit is = 0.46412

Explanation:

Solution:-

- The number of bets made on number "3", N = 170

- He bets on each number "3", k = $1

- The winning pay-off odds : $ ( 35 : 1 )

- The probability of getting number "3" on a spin, p = 1/38

- The total amount paid (C) for n = 170 bets on number "3" are:

C = N*k

C = (170)*($1)

C = $170

- The probability of getting a number "3" on a spin is independent for each trial.

Denote:

- The amount received per win = $ 35

- The number of wins = r

- So the minimum "N" number of wins must be enough to match loss.

Amount Win = Amount Loss

r*$35 = C

r*$36 = C

r = $170 / 36

r = 4.7222 ≈ 5 wins

- So the minimum amount of wins required by r = 10 to make a profit.

- Let a random variable "X" denote the number of times Jorge spins to get number "3" - Number of wins. The probability to get a number "3" on each spin is independent for each trial. Therefore X follows Binomial distribution.

- So, X ~ B ( N , p )

X ~ B ( 170 , 1/38 )

1 - p = 37 / 38

- So we need to determine that Jorge get number "3" at-least r = 5 times. Where the probability mass function for binomial distribution is given below:

`P ( X = r ) = ^NC_r * (p)^r * ( 1 - p )^(^N^ -^ r^ )`

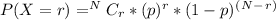
So,

`P ( X \geq 5 ) = 1 - P ( X \leq 4) = 1 - [ P ( X = 0 ) + P ( X = 1 ) + P ( X = 2 ) + P ( X = 3 ) + P ( X = 4 )]\\\\1 - [ (37/38)^1^7^0 + 170*(1/38)*(37/38)^1^6^9 + 170C2*(1/38)^2*(37/38)^1^6^8 + \\\\170C3*(1/38)^3*(37/38)^1^6^7 + 170C4*(1/38)^4*(37/38)^1^6^6 ]\\\\1 - [ 0.01074 + 0.04935 + 0.11271 + 0.17059 + 0.19249]\\\\= 1 - 0.53588\\\\= 0.46412`

- So the probability that Jorge makes a profit is = 0.46412

Note:- The normal approximation to Binomial distribution may be a less cumbersome choice; however, care must be taken to verify the conditions for normal approximation i.e

N*p ≥ 10

With the given data, N = 170 , p = 1/38:

N*p = 170/38 = 4.4737 ≤ 10

Hence, the normal approximation is an invalid choice for the data given.

Answer 2

An estimate of the probability that Jorge will make a profit is (5; 0.496)

Explanation:

The total cost = 170x1 = $170

The payoff is $35 per $1 bet

The number of wins needed to make a profit = 170/35 = 4.86 \approx 5

Probability of winning, P(win), p = 1/38

n = 170

P(Jorge will make a profit) = P(at least 5 wins)

mean = np = 4.47

standard deviation = \sqrt{npq} = 2.09

P(X \geq 5) = 1 - P(X < 5)

P(X < A) = 1 - P(Z < (A - mean)/standard deviation)

After the application of continuity correction,

P(X \geq 5) = 1 - P(Z < (4.5 - 4.47)/2.09)

= 1 - P(Z < 0.01)

= 1 - 0.5040

P(X \geq 5 = 0.496

An estimate of the probability that Jorge will make a profit is (5; 0.496)