Question

A random sample of 100 automobile owners in thestate of Virginia shows that an automobile is driven onaverage 23,500 kilometers per year with a standard deviationof 3900 kilometers. Assume the distribution ofmeasurements to be approximately normal.(a) Construct a 99% confidence interval for the averagenumber of kilometers an automobile is drivenannually in Virginia.(b) What can we assert with 99% confidence about thepossible size of our error if we estimate the averagenumber of kilometers driven by car owners inVirginia to be 23,500 kilometers per year

Answer 1

a) 22497.7 < μ< 24502.3

b) With 99% confidence the possible error will not exceed 1002.3

Explanation:

Given that:

Mean (μ) = 23500 kilometers per year

Standard deviation (σ) = 3900 kilometers

Confidence level (c) = 99% = 0.99

number of samples (n) = 100

a) α = 1 - c = 1 - 0.99 = 0.01

`(\alpha )/(2) =(0.01)/(2)=0.005\\ z_{(\alpha )/(2)}=z_(0.005)=2.57`

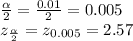
Using normal distribution table,
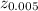`z_{0.005` is the z value of 1 - 0.005 = 0.995 of the area to the right which is 2.57.

The margin of error (e) is given as:

`e= z_(0.005)(\sigma)/(√(n) ) = 2.57*(3900)/(√(100) ) =1002.3`

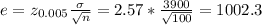
The 99% confidence interval = (μ - e, μ + e) = (23500 - 1002.3, 23500 + 1002.3) = (22497.7, 24502.3)

Confidence interval = 22497.7 < μ< 24502.3

b) With 99% confidence the possible error will not exceed 1002.3