Question

An experiment was performed to compare the abrasive wear of two different laminated materials. Twelve pieces of material 1 were tested by exposing each piece to a machine measuring wear. Ten pieces of material 2 were similarly tested. In each case, the depth of wear was observed. The samples of material 1 gave an average (coded) wear of 85 units with a sample standard deviation of 4, while the samples of material 2 gave an average of 81 and a sample standard deviation of 5. Assume the populations to be approximately normal with equal variances.

a) Can we conclude at the 0.05 level of significance that the abrasive wear of material 1 exceeds that of material 2 by more than 2 units?
b) Repeat part (a) if n1=n2=60.

Answer 1

The calculated value Z= 4.8389> 1.96 at 0.05 level of significance.

The null hypothesis is rejected.

There is significance difference between that the abrasive wear of material 1 not exceeds that of material 2 by more than 2 units

Explanation:

Step:-(1)

Given data the samples of material 1 gave an average (coded) wear of 85 units with a sample standard deviation of 4

Mean of the first sample x₁⁻ =85

standard deviation of the first sample S₁ = 4

Given data the samples of material 2 gave an average of 81 and a sample standard deviation of 5.

Mean of the first sample x₂⁻ =81

standard deviation of the first sample S₂ = 5

Step :-2

Null hypothesis: H₀: there is no significance difference between that the abrasive wear of material 1 exceeds that of material 2 by more than 2 units

Alternative hypothesis :H₁: there is significance difference between that the abrasive wear of material 1 exceeds that of material 2 by more than 2 units

Assume the populations to be approximately normal with equal variances.σ₁² =σ₂²

The test statistic

`Z= \frac{x_(1) -x_(2) }{\sqrt{(S^2_(1) )/(n_(1) ) +(S^2_(2) )/(n_(2) ) } }`

Given n₁=n₂=60.

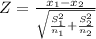
`Z= \frac{85-81 }{\sqrt{((4)^2 )/(60 ) +(5^2 )/(60) } }`

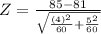
On calculation, we get

Z =
`(4)/(√(0.6833) )`

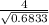
z = 4.8389

The tabulated value Z =1.96 at 0.05 level of significance.

The calculated value Z= 4.8389> 1.96 at 0.05 level of significance.

The null hypothesis is rejected.

Conclusion:-

there is significance difference between that the abrasive wear of material 1 not exceeds that of material 2 by more than 2 units.