Answer:
The calculated value Z= 4.8389> 1.96 at 0.05 level of significance.
The null hypothesis is rejected.
There is significance difference between that the abrasive wear of material 1 not exceeds that of material 2 by more than 2 units
Explanation:
Step:-(1)
Given data the samples of material 1 gave an average (coded) wear of 85 units with a sample standard deviation of 4
Mean of the first sample x₁⁻ =85
standard deviation of the first sample S₁ = 4
Given data the samples of material 2 gave an average of 81 and a sample standard deviation of 5.
Mean of the first sample x₂⁻ =81
standard deviation of the first sample S₂ = 5
Step :-2
Null hypothesis: H₀: there is no significance difference between that the abrasive wear of material 1 exceeds that of material 2 by more than 2 units
Alternative hypothesis :H₁: there is significance difference between that the abrasive wear of material 1 exceeds that of material 2 by more than 2 units
Assume the populations to be approximately normal with equal variances.σ₁² =σ₂²
The test statistic
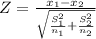
Given n₁=n₂=60.

On calculation, we get
Z =

z = 4.8389
The tabulated value Z =1.96 at 0.05 level of significance.
The calculated value Z= 4.8389> 1.96 at 0.05 level of significance.
The null hypothesis is rejected.
Conclusion:-
there is significance difference between that the abrasive wear of material 1 not exceeds that of material 2 by more than 2 units.