Question

Each vertex of the polygon shown below forms a right angle. The side measurements given are inches. What is the area of the figure?

Answer 1

Given:

Given that each vertex of the polygon forms a right angle.

The measurements of the sides of the polygon were given.

We need to determine the area of the polygon.

Let us divide the polygon into 3 rectangles.

Area of the rectangle can be determined using the formula,
`A=length * width`

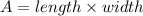
Area of rectangle 1:

The length of rectangle 1 is 17 inches.

The width of rectangle 1 is 8.5 inches.

The area of rectangle 1 is given by

`17 * 8.5 =144.5 \ in^2`

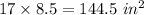
Area of rectangle 2:

The length of rectangle 2 is 16.5 inches.

The width of rectangle 2 is (17 - 9) = 8 inches.

The area of rectangle 2 is given by

`16.5 * 8 =132 \ in^2`

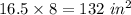
Area of rectangle 3:

The length of rectangle 3 is 13 inches.

The width of rectangle 3 is 11 inches.

The area of rectangle 3 is given by

`13 * 11=143 \ in^2`

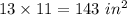
Area of the polygon:

The area of the polygon can be determined by adding the areas of the three rectangles.

Thus, we have;

`Area=144.5+132+143`

`Area=419.5 \ in^2`

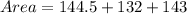
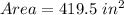
Thus, the area of the figure is 419.5 square inches.

Hence, Option B is the correct answer.