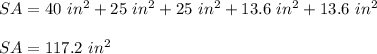Answer:
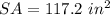
Explanation:
You need to remember the following:
1. The area of a rectangle can be calculated with the following formula:
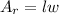
Where "l" is the length and "w" is the width.
2. The area of a triangle can be calculated with the following formula:
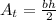
Where "b" is the base and "h" is the height.
Use those formulas to find the area of each face.
Area of the rectangle
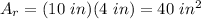
Area of two triangles
There are two equal triangles. Each one has a base of 10 inches and a height of 5 inches. Then, their areas are equal:

The areas of the other two triangles (which are equal) are:
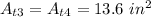
Adding the areas of the faces, you get that the surface area of the rectangular pyramid is: