Question

) Diameter of a star: Assume that the temperature of the Sun is 5800K and the temperature of Sirius A is 10,000K. If the luminosity of Sirius A is 23 times that of the Sun, calculate the radius of Sirius A relative to the Sun. Sirius A is ______ times the size of the Sun. Your answer should be a number in the format (x.x).

Answer 1

Sirius A is 1.608 times the size of the Sun.

Step-by-step explanation:

The radiant flux establishes how much energy an observer or a detector can get from a luminous source per unit time and per unit surface area.

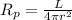`R_(p) = (L)/(4\pi r^2)` (1)

Where
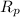`R_(p)` is the radiant power received from the source, L is its intrinsic luminosity and r is the distance.

The Stefan-Boltzmann law is defined as:

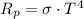`R_(p) = \sigma \cdot T^(4)` (2)

Where
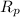`R_(p)` is the radiant power,
`\sigma` is the Stefan-Boltzmann constant and T is the temperature.

Then, equation 2 can be replaced in equation 1

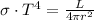`\sigma \cdot T^(4) = (L)/(4\pi r^2)` (3)

Notice that L is the energy emitted per second by the source.

Therefore, r can be isolated from equation 3.

`r^2 = (L)/(4\pi \sigma\cdot T^(4))`

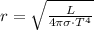`r = \sqrt{(L)/(4\pi \sigma\cdot T^(4))}` (4)

The luminosity of the Sun can be estimated isolating L from equation 3.

`L = (4\pi r^2)(\sigma \cdot T^(4))`

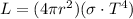
but,
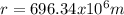`r = 696.34x10^(6)m` and
`T = 5800K`

`L_(Sun) = 4\pi (696.34x10^(6)m)^2(5.67x10^(-8) W/m^(2) K^(4) )(5800K)^(4))`

`L = 3.90x10^(26) W`

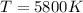
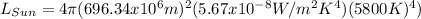
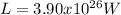
To find the luminosity of Sirius A, the following can be used:

`(L_(SiriusA))/(L_(sun)) = 23`

`{L_(SiriusA)} = (3.90x10^(26) W)(23)`

`{L_(SiriusA)} = 8.97x10^(27)W`

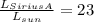
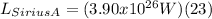
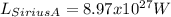
Finally, equation 4 can be used to determine the radius of Sirius A.

`r = \sqrt{(8.97x10^(27)W)/(4\pi (5.67x10^(-8) W/m^(2) K^(4))(10000K)^(4))}`

`r = 1.12x10^(9)m`

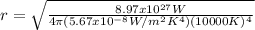
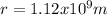
So, Sirius A has a radius of
`1.12x10^(9)m`

`(1.12x10^(9)m)/(696.34x10^(6)m) = 1608`

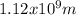
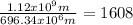
Hence, Sirius A is 1.608 times the size of the Sun.