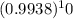Question

The annual rainfall (in inches) in a certain region is normally distributed with µ = 40 and σ = 4. What is the probability that starting with this year, it will take more than 10 years before a year occurs having a rainfall of more than 50 inches? What assumptions are you making?

Answer 1

P( That it will take over 10 years or more of a year with a rainfall above 50inches) = (0.9938)^10

Explanation:

Since the annual rainfall is normally distributed,

Given: that

Mean (µ )= 40

and σ = 4.

Let X be normal random variables of the annual rainfall.

P(that there will be over 10 years or more before a year with a rainfall above 50 inches)

P(>50) = 1-P[X ≤50]

1 - P[X- μ/σ ≤ 50 - 40/4]

=1 - P [Z≤ 5/2]

=1 -Φ(5/2)

=1 - 0.9939

= 0.0062

P( the non occurrence of rainfall above 50 inches)

= 1-0.0062

=0.9938

ASSUMPTION:

P( That it will take over 10 years or more of a year with a rainfall above 50inches) =
`(0.9938)^10`