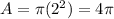2 Answers

Sandeep Bhandari · Answer 1 · 2023-09-07T13:53:24+0000

Answer: 4π

Explanation:

Under the assumption that those are exponents, and your equation is:

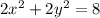
2x^2+2y^2=8

You first must turn this circle equation into standard form. The standard form for the equation of a circle is as follows:

(x-a)^2+(y-b)^2=r^2

For your case, the constants 'a' and 'b' are clearly zero. We have an annoying coefficient of 2 which can be cancelled by dividing both sides by 2:

x^2+y^2=4

If you'd like, we can write this in the following way:

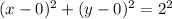
(x-0)^2+(y-0)^2=2^2

So, our circle is centered at the origin (0, 0) and has a radius of 2 units. The area of a circle is given by the formula:

$A=\pi r^2$

$A=\pi (2^2)=4\pi$

Please log in or register to add a comment.