Answer:
Step-by-step explanation:
Radius of the coil, r = 4.2 cm
number of turns, N = 500
resistance in the circuit, R = 640 ohm
The magnetic field is given by
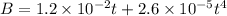
(a) According to the Faraday's law of electromagnetic induction, the magnitude of induced emf is given by

magnetic flux, Ф = N x B x A x Cos 0
Ф = N A B
Differentiate both sides
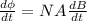

So, the magnitude of induced emf is given by
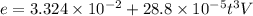
This is the magnitude of induced emf as the function of time.