Question

A surveyor standing 53 space m from the base of a building measures the angle to the top of the building and finds it to be 35 degree. The surveyor then measures the angle to the top of the radio tower on the building and finds that it is 47 degree. How tall is the radio tower

Answer 1

We have been given that a surveyor standing 53 space m from the base of a building measures the angle to the top of the building and finds it to be 35 degree. The surveyor then measures the angle to the top of the radio tower on the building and finds that it is 47 degree.

First of all, we will draw a diagram that will represent our given scenario.

The height of radio tower will be equal to height of building with tower minus height of building.

First of all, we will find the height of the building as:

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(35^(\circ))=(BC)/(53)`

`BC=53\cdot \text{tan}(35^(\circ))`

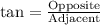
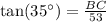
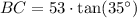
Similarly we will find the height of the building with tower.

`\text{tan}(47^(\circ))=(AC)/(53)`

`AC=53\cdot \text{tan}(47^(\circ))`

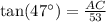
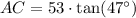
Height of the tower will be
`AC-BC`.

`53\cdot \text{tan}(47^(\circ))-53\cdot \text{tan}(35^(\circ))`

`53\cdot (\text{tan}(47^(\circ))- \text{tan}(35^(\circ)))`

`53\cdot (1.072368710025-0.70020753821)`

`53\cdot (0.372161171815)`

`19.724542106195\approx 19.7`

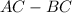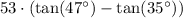
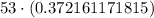
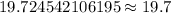
Therefore, the radio tower is approximately 19.7 meters tall.