Answer:
a) The null hypothesis states that the last-minute filers average refund is equal to the early filers refund. The alternative hypothesis states that the last-minute filers average refund is less than the early filers refund.
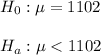
b) P-value = 0.0055
c) The null hypothesis is rejected.
There is enough statistical evidence to support the claim that that the refunds of the individuals that wait until the last five days to file their returns is on average lower than the early filers refund.
d) Critical value tc=-1.96.
As t=-2.55, the null hypothesis is rejected.
Explanation:
We have to perform a hypothesis test on the mean.
The claim is that the refunds of the individuals that wait until the last five days to file their returns is on average lower than the early filers refund ($1102).
a) The null hypothesis states that the last-minute filers average refund is equal to the early filers refund. The alternative hypothesis states that the last-minute filers average refund is less than the early filers refund.
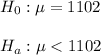
b) The sample has a size n=600, with a sample refund of $1050 and a standard deviation of $500.
We can calculate the z-statistic as:

The degrees of freedom are df=599

The P-value for this test statistic is:
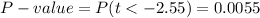
c) Using a significance level α=0.05, the P-value is lower than the significance level, so the effect is significant. The null hypothesis is rejected.
There is enough statistical evidence to support the claim that that the refunds of the individuals that wait until the last five days to file their returns is on average lower than the early filers refund.
d) If the significance level is α=0.025, the critical value for the test statistic is t=-1.96. If the test statistic is below t=-1.96, then the null hypothesis should be rejected.
This is the case, as the test statistic is t=-2.55 and falls in the rejection region.