Question

Individuals filing federal income tax returns prior to March 31 had an average refund of $1102. Consider the population of "last-minute" filers who mail their returns during the last five days of the income tax period (typically April 10 to April 15).

a. A researcher suggests that one of the reasons that individuals wait until the last five days to file their returns is that on average those individuals have a lower refund than early filers. Develop appropriate hypotheses such that rejection of H0 will support the researcher’s contention.

b. For a sample of 600 individuals who filed a return between April 10 and April 15, the sample mean refund was $1050 and the standard deviation was $500. Compute the p-value.

c. Using α =.05, what is your conclusion?

d. Test the hypotheses using the critical value approach (α = 0.025).

Answer 1

a) The null hypothesis states that the last-minute filers average refund is equal to the early filers refund. The alternative hypothesis states that the last-minute filers average refund is less than the early filers refund.

`H_0: \mu=1102\\\\H_a:\mu < 1102`

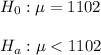
b) P-value = 0.0055

c) The null hypothesis is rejected.

There is enough statistical evidence to support the claim that that the refunds of the individuals that wait until the last five days to file their returns is on average lower than the early filers refund.

d) Critical value tc=-1.96.

As t=-2.55, the null hypothesis is rejected.

Explanation:

We have to perform a hypothesis test on the mean.

The claim is that the refunds of the individuals that wait until the last five days to file their returns is on average lower than the early filers refund ($1102).

a) The null hypothesis states that the last-minute filers average refund is equal to the early filers refund. The alternative hypothesis states that the last-minute filers average refund is less than the early filers refund.

`H_0: \mu=1102\\\\H_a:\mu < 1102`

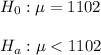
b) The sample has a size n=600, with a sample refund of $1050 and a standard deviation of $500.

We can calculate the z-statistic as:

`t=(\bar x-\mu)/(s/√(n))=(1050-1102)/(500/√(600))=(-52)/(20.41)=-2.55`

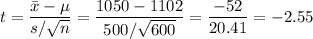
The degrees of freedom are df=599

`df=n-1=600-1=599`

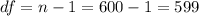
The P-value for this test statistic is:

`P-value=P(t<-2.55)=0.0055`

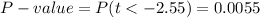
c) Using a significance level α=0.05, the P-value is lower than the significance level, so the effect is significant. The null hypothesis is rejected.

There is enough statistical evidence to support the claim that that the refunds of the individuals that wait until the last five days to file their returns is on average lower than the early filers refund.

d) If the significance level is α=0.025, the critical value for the test statistic is t=-1.96. If the test statistic is below t=-1.96, then the null hypothesis should be rejected.

This is the case, as the test statistic is t=-2.55 and falls in the rejection region.