Question

Your uncle, Larson E. Whipsnade, has asked you for some financial advice. His retirement savings are currently invested as follows: $30,000 in the risk-free asset and $70,000 in GM stock. He wants to know if this is a sensible portfolio. You decide to analyze it based on the CAPM model.

You look in a Beta Book and find that GM stock has a Beta of 1.1 and the R2 of the regression is 0.40. Microsoft stock has a Beta of 0.8 and the R2 of the regression is 0.30. Suppose further that the correlation between the return to GM stock and the return to Microsoft stock is 0.3.

If the market return have the standard deviation 20%, compute the variance and standard deviation in current portofolio.

Answer 1

Step-by-step explanation:

If the market return was known, our calculation would have been easier

`As Portfolio variance = (W1S1)2+(W2S2)2+(W3S3)2+2W1S1W2S2P12+2W2S3W3S3P23+2W1S1W3S3P13`

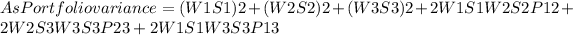
Where W=Weight, S= Standard Deviation, P=Covariance

1= General Motors, 2= Microsoft and 3= Risk free Asset

It gets easier as

All Weights (W) are known, W1= 0.4, W2= 0.4 and W3= 0.2

S1 and S2 can be easily found out and S3 is zero (Standard Deviation of Risk Free Asset)

Covariance (P) of any stock with risk free asset is zero, so P23 and P13 are zero

We need S1, S2, P12

+As Beta of GM = 1.1 and Standard Deviation of Market = 0.2 and R2 of GM = 0.4

We can find S1 by the formula Beta=(Sd of Stock/Sd of Market) * RGM2

Standard Deviation of Gm (S1) = BetaGM * (Standard Deviation of Market / RGM2 )

= 1.1 * (0.2 / 0.4)

= 0.55

+As Beta of Microsoft = 0.8 and Standard Deviation of Market = 0.2 and R2 of Microsoft = 0.3

We can find S2 by the formula Beta=(Sd of Stock/Sd of Market) * RM2

Standard Deviation of Gm (S2) = BetaM * (Standard Deviation of Market / RM2 )

= 0.8 * (0.2 / 0.3)

= 0.5333333

+As Correlation between Microsoft and General Motors is given as 0.3 and S1and S2 are known from above,

Covariance of General Motors and Microsoft (P12) can be found out from the formula

Corelation 12 = Covariance 12/(Standard Deviation 1 * Standard Deviation2)

So Covariance of the Stocks P12 = Corelation12 * S1 * S2

= 0.3 * 0.55 * 0.533

= 0.087945 or 0.088

So Portfolio Variance = (W1S1)2+(W2S2)2++2W1S1W2S2P12

Note

[any term with S3 gets cancelled hence, omitted for easier comprehension]

= (0.4*0.55)2+(0.4*0.533)2+2(0.4)(0.55)(0.4)(0.533)(0.88)

= 0.0484 + 0.04545 + 0.008255

= 0.102105 or 0.102

= √0.102

= 0.3195 or 0.32