Question

The Royal Fruit Company produces two types of fruit drinks. The first type is 35% pure fruit juice, and the second type is 60% pure fruit juice. The company is attempting to produce a fruit drink that contains 55% pure fruit juice. How many pints of each of the two existing types of drink must be used to make 140 pints of a mixture that is 55% pure fruit juice?

Note that the ALEKS graphing calculator can be used to make computations easier.
Firstfruitdrink: pints Secondfruitdrink: pints

Answer 1

28 pints, 112 pints

Explanation:

GIVEN: The Royal Fruit Company produces two types of fruit drinks. The first type is
`35\%` pure fruit juice, and the second type is
`60\%` pure fruit juice. The company is attempting to produce a fruit drink that contains
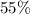`55\%` pure fruit juice.

TO FIND: How many pints of each of the two existing types of drink must be used to make
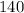`140` pints of a mixture that is
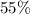`55\%` pure fruit juice.

SOLUTION:

Let the quantity of first type of juice be
`x\text{ pints}`

Quantity of second type of juice
`=140-x\text{ pints}`

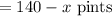
Concentration of pure juice in final mixture
`=55\%`

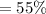
Now,

The concentration of pure juice in final mixture is sum of concentrations of pure juice in first and second type of juice

`(55)/(100)*140=(35)/(100)* x + (60)/(100)* (140-x)`

`25x=700`

`x=28`

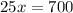
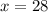
Quantity of first type of juice
`=28\text{ pints}`

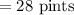
Quantity of second type of juice
`=140-28=112\text{ pints}`

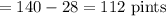
Hence quantity of first and second type of juice is 28 pints and 112 pints respectively.