Answer:
The significance level α is 0.02.
Explanation:
A hypothesis test for single mean can be performed to determine whether the average starting salary for a 21-25 year old college grad exceeds $52,000 per year.
The hypothesis is defined as follows:
H₀: The average starting salary for a 21-25 year old college grad does not exceeds $52,000 per year, i.e. µ ≤ 52,000.
Hₐ: The average starting salary for a 21-25 year old college grad exceeds $52,000 per year, i.e. µ > 52,000.
The information provided is:
σ = $5,745
n = 65
Also, if
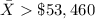 then the null hypothesis will be rejected.
then the null hypothesis will be rejected.
Here, we need to compute the value of significance level α, the type I error probability.
A type I error occurs when we reject a true null hypothesis (H₀).
That is:
α = P (type I error)
α = P (Rejecting H₀| H₀ is true)
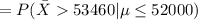
![=P[(\bar X-\mu_(0))/(\sigma/√(n))>(53460-52000)/(5745/√(65))]](https://img.qammunity.org/2021/formulas/mathematics/college/yyc16hh5zjw39sv2zdy5d0p1lhm2qaz9kc.png)

*Use a z-table for the probability.
Thus, the significance level α is 0.02.