Question

Functions f(x) and g(x) are shown below:

f(x) = x2
g(x) = x2 - 8x + 1
In which direction and by how many units should f(x) be shifted to obtain g(x)? (1 poi
Left by 4 units
Right by 4 units
Left by 8 units
Right by 8 units
​

Answer 1

B. Right by 4 units

Explanation:

Answer 2

f(x) should shifted Right by 4 units to obtain g(x) ⇒ B

Explanation:

Let us put g(x) in the form of g(x) = (x - h)² + k, where h is the the horizontal shift (x - h) to right, (x + h) to left and k is the vertical shift (k) up and (-k) down

In the quadratic function y = ax² + bx + c, h =
`-(b)/(2a)` and k = y at x = h

∵ g(x) = x² - 8x + 1

∵ a is the coefficient of x² and b is the coefficient of x

∴ a = 1 and b = -8

∵ h =
`-(b)/(2a)`

∴ h =
`-(-8)/(2(1))=(8)/(2)`

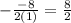
∴ h = 4

∵ k = g(x) at x = h

- Substitute x by 4 in g(x) to find k

∴ k = (4)² - 8(4) + 1 = 16 - 32 + 1

∴ k = -15

- Substitute them in the form of g(x) = (x - h)² + k

∴ g(x) = (x - 4)² + (-15)

∵ h is the horizontal shift

∵ (x - h) means shift to right h units

∵ f(x) = x²

∵ g(x) = (x - 4)² + (-15)

- That means f(x) is shifted 4 units to the right

∴ f(x) should shifted right by 4 units to obtain g(x)