Question

A procurement specialist has purchased 23 resistors from vendor 1 and 30 resistors from vendor 2. Let represent the vendor 1 observed resistances, which are assumed to be normally and independently distributed with mean 120 ohms and standard deviation 1.7 ohms. Similarly, let represent the vendor 2 observed resistances, which are assumed to be normally and independently distributed with mean 125 ohms and standard deviation of 2.0 ohms. What is the sampling distribution of ? What is the standard error of ? The sampling distribution of is What is thesampling distribution of X1 − X2? What is the standard errorof X1 − X2?

Answer 1

The standard error( X1 − X2 ) = 0.547

Explanation:

Step:-(1)

Given a procurement specialist has purchased 23 resistors

Given normally and independently distributed with mean 120 ohms and standard deviation 1.7

mean of the Population of the vendor 1 is μ₁ = 120 ohms

Standard deviation of the Population the vendor 1 is σ₁ = 1.7 ohms

similarly represent the vendor 2 observed resistances, which are assumed to be normally and independently distributed with mean 125 ohms and standard deviation of 2.0

mean of the Population of the vendor 2 is μ₂ = 120 ohms

Standard deviation of the Population the vendor 2 is σ₂ = 1.7 ohms

The standard error of the difference of two means

Se( X1 − X2) =
`\sqrt{(σ^2_(1) )/(n_(1) ) +(σ^2_(2) )/(n_(1) ) }`

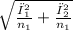
Here σ₁ = 1.7 ohms and σ₂ = 2 ohms and n₁=n₂ =n = 23 resistors

se(X1 − X2) =
`\sqrt{(1.7^2)/(23 ) +(2^2 )/(23) }`

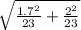
se(X1 − X2) = √0.2995

= 0.547

Conclusion:-

The standard error of X1 − X2 = 0.547