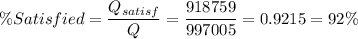Question

Galaxy Co. distributes wireless routers to Internet service providers. Galaxy procures each router for $75 from its supplier and sells each router for $125. Monthly demand for the router is a normal random variable with a mean of 100 units and a standard deviation of 20 units. At the beginning of each month, Galaxy orders enough routers from its supplier to bring the inventory level up to 100 routers. If the monthly demand is less than 100, Galaxy pays $15 per router that remains in inventory at the end of the month. If the monthly demand exceeds 100, Galaxy sells only the 100 routers in stock. Galaxy assigns a shortage cost of $30 for each unit of demand that is unsatisfied to represent a loss-of-goodwill among its customers. Management would like to use a simulation model to analyze this situation.

a. What is the average monthly profit resulting from its policy of stocking 100 routers at the beginning of each month?
b. What percentage of total demand is satisfied?

Answer 1

Galaxy Co. distributes wireless routers to Internet service providers and stocks 100 routers at the beginning of each month. The average monthly profit and the percentage of total demand satisfied can be calculated based on the different scenarios. The profit and satisfaction percentage depend on the monthly demand, which is a normally distributed random variable with a mean of 100 units and a standard deviation of 20 units.

Step-by-step explanation:

Galaxy Co. distributes wireless routers to Internet service providers. Each router is procured for $75 and sold for $125. The monthly demand for the router is normally distributed, with a mean of 100 units and a standard deviation of 20 units. The company stocks 100 routers at the beginning of each month and incurs a cost of $15 for each router that remains in inventory at the end of the month if the demand is less than 100. If the demand exceeds 100, only the 100 routers in stock are sold. The shortage cost of $30 is assigned for each unit of unsatisfied demand.

a. The average monthly profit resulting from this policy can be calculated by considering the different scenarios:

1. If the monthly demand is 100 units or less, the profit is ($125 - $75) x 100 - $15 x (100 - demand);
2. If the monthly demand is more than 100 units, the profit is ($125 - $75) x 100 - $15 x 0 - $30 x (demand - 100);
3. If the demand is normally distributed, the average monthly profit can be calculated by considering the probabilities of different demand levels and corresponding profits. Using the mean and standard deviation of the demand, the average monthly profit can be determined.

b. The percentage of total demand that is satisfied can be calculated by considering the different scenarios:

1. If the monthly demand is 100 units or less, the percentage of total demand satisfied is 100%;
2. If the monthly demand is more than 100 units, the percentage of total demand satisfied is 100 / demand x 100;
3. If the demand is normally distributed, the average percentage of total demand satisfied can be determined by considering the probabilities of different demand levels and corresponding percentages of total demand satisfied. Using the mean and standard deviation of the demand, the average percentage of total demand satisfied can be calculated.

Answer 2

Simulation results:

- the average monthly profit resulting from its policy of stocking 100 routers at the beginning of each month is $4237.

- percentage of total demand is satisfied: 92%.

Step-by-step explanation:

We have to consider three factors to calculate the profit:

1. Sales. Every unit sold adds (125-75)=$50 to the profit. We have to consider the condition that the maximum amount of units that can be sold is 100 units.
2. The remains cost. If the monthly demand is under 100 units, the profit is reduced by $15 per each remaining unit.
3. The shortage cost. For each unit demanded that exceeds the 100 units, the profit is reduced by $30.

The equation can be expressed as:

`Profit=50*Max(Q;100)-15*Max(100-Q;0)-30*Max(Q-100;0)`

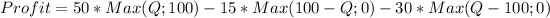
A simulation with 10,000 trials is done, and the average monthly profit calculated for this policy is $4237.

The demand was calculated with the Excel function INT(NORMINV(RAND(),100,20)), to mimic a normal distribution with mean 100 and standard deviation 20.

b) The satisified demand is calculated for each trial as the minimum value between Q (quantity demanded) and 100, as if Q is bigger than 100, only 100 units of the demand are satisfied.

The percentage of total demand satisfied is:

`\%Satisfied=(Q_(satisf))/(Q)=(918759)/(997005)=0.9215=92\%`