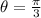2 Answers

Rexcfnghk · Answer 1 · 2021-09-21T04:56:57+0000

Given:

Given that the radius of the circle is 3 units.

The arc length is π.

The central angle is θ.

We need to determine the expression to find the measure of θ in radians.

Expression to find the measure of θ in radians:

The expression can be determined using the formula,

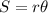
$S=r \theta$

where S is the arc length, r is the radius and θ is the central angle in radians.

Substituting S = π and r = 3, we get;

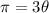
$\pi=3 \theta$

Dividing both sides of the equation by 3, we get;

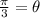
$(\pi)/(3)=\theta$

Thus, the expression to find the measure of θ in radians is
$\theta=(\pi)/(3)$

Please log in or register to add a comment.