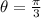Given:
Given that the radius of the circle is 3 units.
The arc length is π.
The central angle is θ.
We need to determine the expression to find the measure of θ in radians.
Expression to find the measure of θ in radians:
The expression can be determined using the formula,
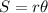
where S is the arc length, r is the radius and θ is the central angle in radians.
Substituting S = π and r = 3, we get;
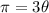
Dividing both sides of the equation by 3, we get;
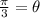
Thus, the expression to find the measure of θ in radians is