Answer:
(a)
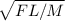
(b)
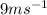
Step-by-step explanation:
(a)
The speed of the wave depends on the type of the material. Here we have neoprene sheet so the speed of the wave will depend on the linear density of neoprene sheet. Linear Density is defined as Mass per unit length of the material (as materials of same type can have different thickness). The symbol used for the Linear Density is .
μ = Mass of the sheet / Length of the sheet
The speed of the wave in such material can be be found by using the equation:
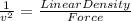 (where v is speed)
(where v is speed)
The equation can be rearranged:
v =
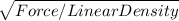
so,
v = sqrt(F/μ)
v = sqrt(F/ (M/L))
v =
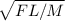 (answer)
(answer)
(b)
Putting the values
F = 81 N
M = 4kg
L = 4m
v =
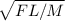
v = 9m/s