X-5=y, xy+4=0, then what is 4x^(2) +4y^(2)

Question

`x-5=y, xy+4=0,` then what is
`4x^(2) +4y^(2)`

Answer 1

68

Explanation:

`\textsf{Equation 1}:\:x-5=y`

`\textsf{Equation 2}:\:xy+4=0`

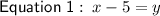
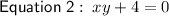
Substitute Equation 1 into Equation 2:

`\implies x(x-5)+4=0`

`\implies x^2-5x+4=0`

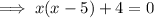
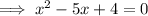
Factorize:

`\implies (x-1)(x-4)=0`

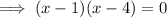
Therefore:

`x=1, x=4`

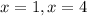
Substitute found values of
`x` into Equation 1 and solve for
`y`:

`x=1\implies 1-5=-4`

`x=4\implies 4-5=-1`

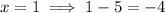
Substitute found values into
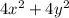`4x^2+4y^2` and solve:

`\textsf{For}\:(1,-4)\implies 4(1)^2+4(-4)^2=68`

`\textsf{For}\:(4,-1)\implies 4(4)^2+4(-1)^2=68`

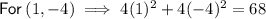
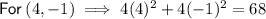
Note: As
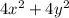`4x^2+4y^2`, the values of x and y can be interchanged, so no need to input both sets of ordered pairs into the equation to solve.

Answer 2

68

Given:

• x - 5 = y ........ eq 1

• xy + 4 = 0 ...... eq 2

Substitute equation 1 into 2

• x(x - 5) + 4 = 0

• x² - 5x + 4 = 0

• x² - 4x - x + 4 = 0

• x(x-4) -1(x-4) = 0

• (x-4)(x-1) = 0

• x = 1, 4

Find y:

y = x - 5

y = 1 - 5 (when x is 1)

y = -4

========

y = x - 5

y = 4 - 5 (when x is 4)

y = -1

Then 4x² + 4y²:

• 4(1)² + 4(-4)²

• 4 + 64

• 68