Question

6. Air at 300°C and 130kPa ows through a horizontal 7-cm ID pipe at a velocity of 42.0m/s. (a) Calculate _ Ek W, assuming ideal-gas behavior. (b) If the air is heated to 400°C at constant pressure, what is Δ _ Ek _ Ek 400°C _ Ek 300°C? (c) Why would it be incorrect to say that the rate of transfer of heat to the gas in Part (b) must equal the rate of change of kinetic energy?

Answer 1

a)
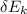`\delta E_k` = 112.164 W

b)
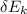`\delta E_k` = 42.567 W

c) From what we've explained in part b; increase in temperature of the system is caused by rate of heat transfer . Therefore, not all heat is used to increase kinetic energy. Hence, since not all the heat is used to increase the kinetic energy . It is not valid and it is incorrect to say that rate of heat transfer is equal to the change in kinetic energy.

Step-by-step explanation:

The given data include:

Inlet diameter
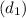`(d_1)` = 7 cm = 0.7 m

Inlet velocity
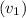`(v_1)` = 42 m/s

Inlet pressure
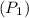`(P_1)` = 130 KPa

Inlet temoerature
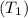`(T_1)` = 300°C = (300 + 273.15) = 573.15 K

a) Assuming Ideal gas behaviour

Inlet Volumetric flowrate
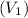`(V_1)` = Inlet velocity
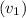`(v_1)` × area of the tube

`= v_1*((\pi)/(4))0.07^2\\\\= 0.161635 \ m^3/s`

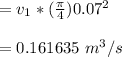
Using Ideal gas law at Inlet 1

`P_1V_1 =nRT_1`

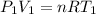
where ; n = molar flow rate of steam

making n the subject of the formula; we have:

`n = (P_1V_1)/(RT_1)`

`n = (130*42)/(8.314*573.15)`

`n= 4.4096*10^(-3) \ Kmol/s`

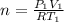
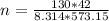
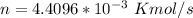
Moleular weight of air = 28.84 g/mol

The mass flow rate = molar flowrate × molecular weight of air

`= 4.4096*10^(-3) \ * 28.84\\= 0.12717 \ kg/s`

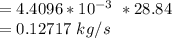
Finally: the kinetic energy at Inlet
`(\delta E_k) = (1)/(2)*mass \ flowrate *v_1^2`

=
`0.5*0.12717*42^2`

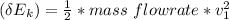
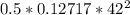
= 112.164 W

b) If the air is heated to 400°C;

Then temperature at 400°C = (400 + 273.15)K = 673.15 K

Thee pressure is also said to be constant ;

i.e
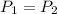`P_1= P_2` = 130 KPa

Therefore; the mass flow rate is also the same ; so as the molar flow rate:

Thus;
`n= 4.4096*10^(-3) \ Kmol/s`

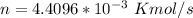
Using Ideal gas law at Inlet 2

`P_2V_2 = nRT_2`

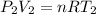
making
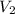`V_2` the subject of the formula; we have:

`V_2 = (nRT_2)/(P_2)`

`V_2 = (4.4906*10^(-3)*8.314*673.15)/(130)`

`V_2 = 0.189836 \ m^3/s`

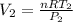
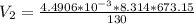
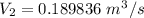
Assuming that the diameter is constant

`d_1 = d_2 = 0.07 \ cm`

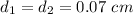
Now; the velocity at outlet =
`(V_2)/((\pi)/(4)d_2^2)`

=
`(0.0189836)/((\pi)/(4)(0.07)^2)`

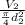
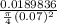
= 49.33 m/s

Change in kinetic energy
`\delta E_k` =
`(1)/(2)*mass \ flowrate * \delta V`

=
`0.5*0.12717 *(49.33^2 -42^2)`

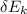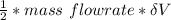
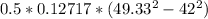
= 42.567 W

c).

From what we've explained in part b; increase in temperature of the system is caused by rate of heat transfer . Therefore, not all heat is used to increase kinetic energy. Hence, since not all the heat is used to increase the kinetic energy . It is not valid and it is incorrect to say that rate of heat transfer is equal to the change in kinetic energy.

Answer 2

Check the explanation

Step-by-step explanation:

kindly check the attached image below to see the answer to question A and B

(c) The energy balance equation if the pressure is constant (ΔE=0) is,

ΔE= ΔU + Δ
`E_(k)`

From the above relation, it is clear that some heat energy used to raises the temperature of the air.

Hence, the internal energy is not equal to zero. Therefore, the rate of transfer of heat to air is not equal to the rate of thane in kinetic energy of the air.

That is ΔE ≠ Δ
`E_(k)`