Question

Graph a line that contains the point (-5,-3) and has a slope of -2

Answer 1

-->

Explanation:

Graph (-5,-3) and use the slope, -2, to find another point. -2 can also be written as
`-(2)/(1)`

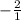
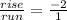`(rise)/(run) =(-2)/(1)` and
`(rise)/(run) =(2)/(-1)` **

Use both. This works because either way, they will lie on the same line with the same slope. So, starting at (-5,-3), go down two points (-)* and to the left 1 (+)*, then, starting at (-5,-3) again, go up two points (+)* then to the right 1 point (-)*.

* If the number is negative, you either go down or to the right. If the number is positive, you go up and to the left.

**Rise over run refers to the change in the y-axis and the change in the x-axis:
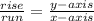`(rise)/(run) =(y-axis)/(x-axis)`. Only one number is negative because, if both were negative, that would make a positive number, but the slope is -2, not 2.

Another way you could do this is by finding points first. All you need to do is turn the slope into a "point". Remember, 2 is the y and 1 is the x:

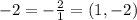`-2=-(2)/(1) = (1,-2)` and
`(-1,2)`

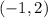
Then, using (-5,-3) and your new points, add them separately:

`(-5,-3)+(1,-2)\\(-5+1,-3+(-2))\\(-5+1,-3-2)\\(-4,-5)`

(-4,-5) is one point

`(-5,-3)+(-1,2)\\(-5+(-1),-3+2)\\(-5-1,-3+2)\\(-6,-1)`

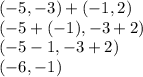
(-6,-1) is another point. Connect the three points. You can check your work on the graph: