Answer:
-->
Explanation:
Graph (-5,-3) and use the slope, -2, to find another point. -2 can also be written as
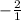
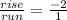 and
and
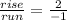 **
**
Use both. This works because either way, they will lie on the same line with the same slope. So, starting at (-5,-3), go down two points (-)* and to the left 1 (+)*, then, starting at (-5,-3) again, go up two points (+)* then to the right 1 point (-)*.
* If the number is negative, you either go down or to the right. If the number is positive, you go up and to the left.
**Rise over run refers to the change in the y-axis and the change in the x-axis:
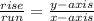 . Only one number is negative because, if both were negative, that would make a positive number, but the slope is -2, not 2.
. Only one number is negative because, if both were negative, that would make a positive number, but the slope is -2, not 2.
Another way you could do this is by finding points first. All you need to do is turn the slope into a "point". Remember, 2 is the y and 1 is the x:
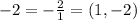 and
and
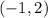
Then, using (-5,-3) and your new points, add them separately:
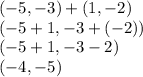
(-4,-5) is one point
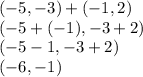
(-6,-1) is another point. Connect the three points. You can check your work on the graph: