Answer:
t = 2.175 s (3 dp)
t = 0.575 s (3 dp)
Explanation:
Given equation:
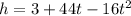
To find all values of t for which the ball's height is 23 ft, substitute h = 20 into the equation and solve for t:

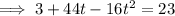
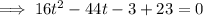
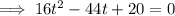
Factor out common term 4:
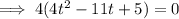
Divide both sides by 4:
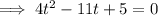
Quadratic formula
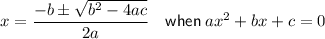
Use the quadratic formula to solve for t:
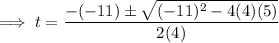
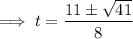
Therefore,
- t = 2.175 s (3 dp)
- t = 0.575 s (3 dp)