Question

Two blocks are connected to identical ideal springs and are oscillating on a horizontal frictionless surface. Block A has mass m, and its motion is represented by the graph of position as a function of time shown above on the left. Block B’s motion is represented above on the right. Which of the following statements comparing

block B to block A is correct?

(A) Because block B covers more distance per cycle than block A, block B takes more time to complete each
cycle.
(B) Because the spring attached to block B is initially stretched a greater distance, the spring constant is smaller
and therefore block B has a slower average speed than block A does.
(C) Because block B has more mass, it has a slower average speed than block A does.
(D) Because block B has more mass, its acceleration is smaller than that of block A at any given displacement
from the equilibrium position.

Answer 1

Hi there!

We can begin by identifying key characteristics of both graphs.

Graph A.

Looking at the graph, we can see that the maximum distance (amplitude) is 10 cm (0.1 m). Additionally, its period (T) is 2 seconds (one full cycle).

We also know that:

`T = 2\pi \sqrt{(m)/(k)}`

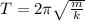
We can use this equation to compare with the other graph. Notice how the period does NOT depend on how far the spring is stretched. We can eliminate choice A for this reason.

Graph B.

The amplitude is 20 cm (0.2 m), and each period is 4 seconds.

We can now eliminate choice B because the springs are identical, so their spring constants are equal. Distance stretched has no impact on the spring constant.

For the other choices, we must look at forces and work.

Recall that:
Spring potential energy =
`(1)/(2)kx^2`

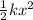
Kinetic energy =
`(1)/(2)mv^2`

Using the work-energy theorem:

`(1)/(2)kx^2 = (1)/(2)mv^2`

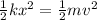
Even if the mass of Block B is greater, its displacement is larger than that of Block A. Since displacement is squared in this equation, it would have a greater effect on the speed. Thus, Choice C is incorrect.

Using Hooke's Law:

`\Sigma F = -kx\\\\ma = -kx\\`

`a = (-kx)/(m)`

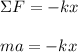
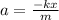
If the mass is greater, the acceleration will be smaller. Choice D is correct.