Question

In a physics lab, light with a wavelength of 540 nm travels in air from a laser to a photocell in a time of 16.5 ns. When a slab of glass with a thickness of 0.820 m is placed in the light beam, with the beam incident along the normal to the parallel faces of the slab, it takes the light a time of 21.5 ns to travel from the laser to the photocell.

What is the wavelength of the light in the glass? Use 3.00×10^8 m/s for the speed of light in a vacuum.

Answer 1

189.47nm

Step-by-step explanation:

We can solve this problem by taking into account the time that light takes in crossing the distance between the laser and the photocell, and the time in crossing the slab.

By using the values of c and 16.5ns we can calculate the value of d

`d=(3*10^(8)m/s)(16.5*10^(-9)s)=4.95m`

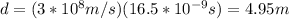
We have to compute the time that light takes in crossing d-0.820m:

`4.95m-0.820m=4.13m\\\\t=(4.13m)/(3*10^8m/s)=6.22*10^(-8)s=13.7ns`

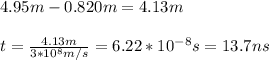
Now, we can calculate the speed of the light in the slab by using the time difference between 21.5 ns and 13.7ns:

`\Delta t=21.5ns-13.7ns=7.8ns\\\\v_l=(0.82m)/(7.8ns)=1.05*10^8m/s`

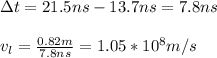
Then, the index of refraction will be:

`n=(c)/(v_l)=2.85`

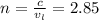
Finally, we have that:

`(\lambda_2)/(\lambda_1)=(n_1)/(n_2)\\\\\lambda_2=\lambda_1 (n_1)/(n_2)=(540nm)(1.00)/(2.85)=189.47nm`

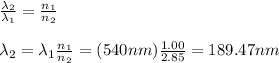
hope this helps!!