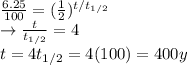Answer:
400 years
Step-by-step explanation:
The equation that describes the decay of a radioactive sample is:
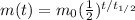 (1)
(1)
where
m(t) is the amount of sample left at time t
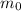 is the initial amount of the sample
is the initial amount of the sample
 is the half-life, which is the time taken for the sample to halve
is the half-life, which is the time taken for the sample to halve
In this problem we have:
 is the half-life of Nickel-63
is the half-life of Nickel-63
After a time t, the amount of sample left is 6.25% of the original one, which means that
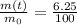
So we can rewrite the equation (1) and solving for t to find the time: