Question

A prallelogram has a height of 4 cm and a base of 8 cm. After being dilated, the resulting image has an area of 8 cm2. What scale factor was applied to the base and height of the original parallelogram?​

Answer 1

The scale factor applied was 1/2

Explanation:

step 1

Find the area of the original parallelogram

A=bh

substtute the given values

`A=(8)(4)=32\ cm^2`

step 2

Find the scale factor

we know that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Let

z ----> scale factor

x ---> area of the dilated parallelogram

y ---> area of the original paeallelogram

so

`z^2=(x)/(y)`

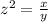
we have

`x=8\ cm^2\\y=32\ cm^2`

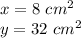
substitute

`z^2=(8)/(32)`

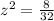
simplify

`z^2=(1)/(4)`

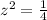
therefore

`z=(1)/(2)`

The scale factor applied was 1/2