Answer:
(a) The probability that the mean weight of the sample is less than 3.05 pounds is 0.8413.
(b) The value for which the mean weight exceed with probability 0.99 is 2.88 pounds.
Explanation:
We are given that the weight of adobe bricks for construction is normally distributed with a mean of 3 pounds and a standard deviation of 0.25 pound.
Assume that the weights of the bricks are independent and that a random sample of 25 bricks is chosen.
Let
 = sample mean weight of the bricks
= sample mean weight of the bricks
The z-score probability distribution for sample mean is given by;
Z =
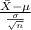 ~ N(0,1)
~ N(0,1)
where,
 = population mean weight of bricks = 3 pounds
= population mean weight of bricks = 3 pounds
 = standard deviation = 0.25 pounds
= standard deviation = 0.25 pounds
n = sample of bricks = 25
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
(a) Probability that the mean weight of the sample is less than 3.05 pounds is given by = P(
 < 3.05 pounds)
< 3.05 pounds)
P(
 < 3.05 pounds) = P(
< 3.05 pounds) = P(
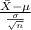 <
<
 ) = P(Z < 1) = 0.8413
) = P(Z < 1) = 0.8413
So, in the z table the P(Z
 x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1 in the z table which has an area of 0.84134.
x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1 in the z table which has an area of 0.84134.
Hence, the probability that the mean weight of the sample is less than 3.05 pounds is 0.8413.
(b) Now, we have to find the value for which the mean weight exceed with probability 0.99, that means;
P(
 > x) = 0.99 {where x is the required value}
> x) = 0.99 {where x is the required value}
P(
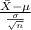 >
>
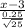 ) = 0.99
) = 0.99
P(Z >
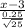 ) = 0.99
) = 0.99
1 - P(Z

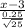 ) = 0.99
) = 0.99
P(Z

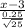 ) = 1 - 0.99
) = 1 - 0.99
P(Z

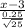 ) = 0.01
) = 0.01
Now, in the z table, the critical value of x for which the probability area is less than 0.01 is -2.3263, i.e.;
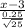 = -2.3263
= -2.3263
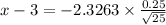
 = 3 - 0.116315 = 2.88 pounds
= 3 - 0.116315 = 2.88 pounds
Therefore, the value for which the mean weight exceed with probability 0.99 is 2.88 pounds.