Question

Calls arrive at Lynn Ann Fish’s hotel switchboard at a rate of 2 per minute. The average time to handle each is 20 seconds. There is only one switchboard operator at the current time. The Poisson and negative exponential distributions appear to be relevant in this situation

a) What is the probability that the operator is busy?
b) What is the average time that a customer must wait before reaching the operator?
c) What is the average number of calls waiting to be answered?

Answer 1

Part A. Compute the probability that operator of the hotel is busy.

The call arrives at Lynn Ann Hotel at the rate of 2/min.

Therefore, 2 min = 120 customers per hour

Thus, the call is serviced by the operator at a rate of 20 seconds per customer.

Therefore,

P = 180 customers per hour

Probability that the operator will be busy:

P = λ / µ

P= 120 / 180

P = 0.67

Therefore, the probability that the hotel operator is busy is 0.67 hours

Part B. Determine the average time customer must wait:

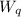`W_(q)` = λ / µ (µ - λ)

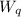`W_(q)` = 120 / 180(180 - 120)

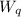`W_(q)` = 120 / 180(60)

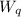`W_(q)` = 120 / 10,800

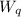`W_(q)` = 0.011

Thus, the average wait time for the customer is 0.011 hours

Part C. Determine the average number of call waiting:

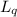`L_(q)` = λ^2 / µ (µ - λ)

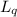`L_(q)` = 120^2 / 180 (180 - 120)

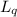`L_(q)` = 14,400 / 180 (60)

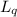`L_(q)` = 14,400 / 10,800

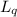`L_(q)` = 1.33

Thus, the average waiting call to be answered is 1.33 hours