Question

Use a sample n= 840 , p = 0.25, and a confidence level to construct a confidence interval estimate of the population proportion ,p.

Answer 1

Answer:0.225<p<0.275

Explanation:

gradpoint

Answer 2

Answer: The confidence interval would be (0.221, 0.279).

Explanation:

Since we have given that

n = 840

p = 0.25

q = 1 - p =
`1-0.25=0.75`

Let 95% level confidence, z = 1.96

Margin of error is given by :

`z* \sqrt(pq)/(n)}=1.96* \sqrt{(0.25* 0.75)/(840)}\\\\=1.96* 0.0149\\\\=0.029`

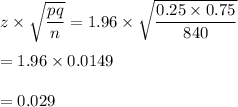
So, confidence interval would be

`p\pm \text{Margin of error}\\\\=0.25\pm 0.029\\\=(0.25-0.029,0.25+0.029)\\\\=(0.221,0.279)`

Hence, the confidence interval would be (0.221, 0.279).